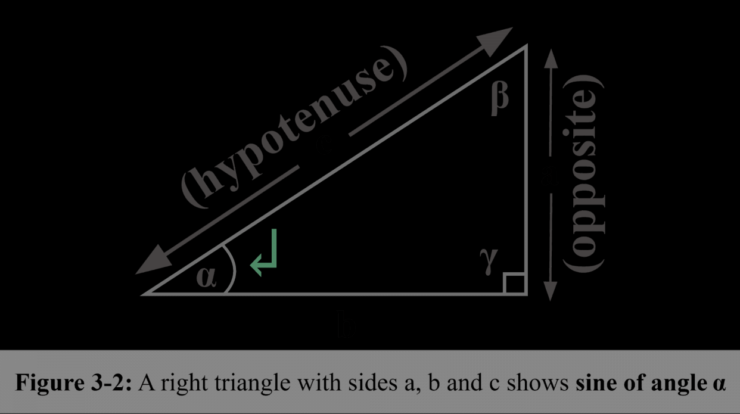
Sine definition – Embark on a captivating journey into the realm of trigonometry, where we unravel the mysteries of the sine function. Defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle, sine plays a pivotal role in various fields, from physics to music.
Delving deeper, we’ll explore the mathematical formula for sine, its range and period, and its practical applications in real-world scenarios. Prepare to be enlightened as we dissect the graph of sine, analyze its key features, and uncover the secrets of the inverse sine function.
Sine: A Fundamental Trigonometric Function
The sine function is a fundamental trigonometric function that plays a vital role in various fields. It is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right-angled triangle.
Definition of Sine
Mathematically, the sine of an angle θ (theta) in a right-angled triangle is given by the formula:
sin(θ) = opposite / hypotenuse
The range of the sine function is [-1, 1], and its period is 2π.
Applications of Sine, Sine definition
Sine is widely used in real-world applications, including:
- Physics:Describing oscillatory motion, such as the motion of a pendulum or a spring.
- Engineering:Designing structures and machines that experience periodic forces, such as bridges and aircraft.
- Music:Determining the pitch and frequency of musical notes.
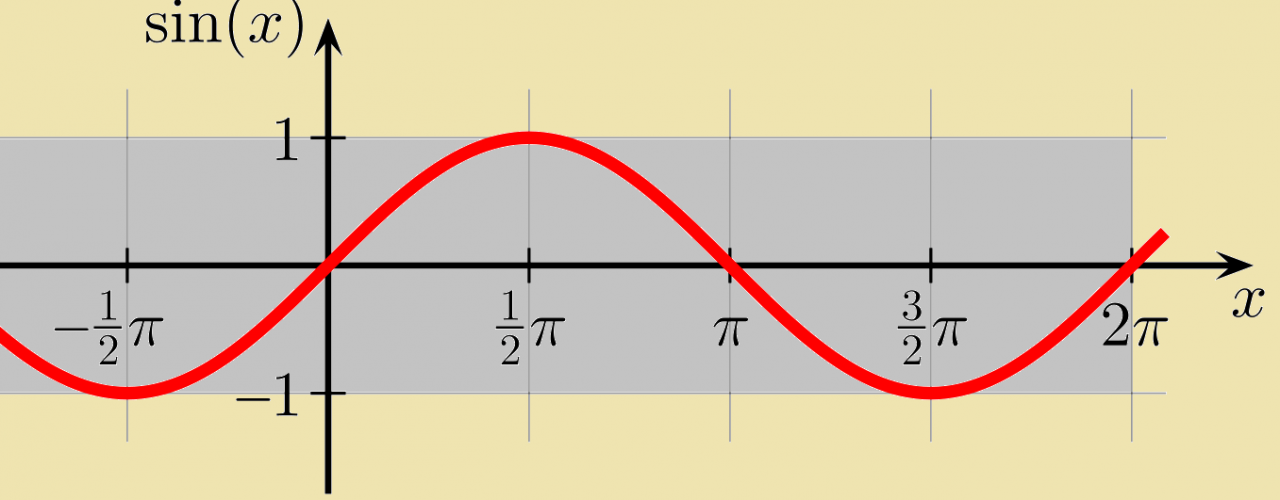
Graph of Sine
The graph of the sine function is a smooth, periodic curve that oscillates between -1 and 1. Key features of the sine graph include:
- Amplitude:The maximum value of the function, which is 1.
- Period:The distance between two consecutive peaks or troughs, which is 2π.
- Frequency:The number of cycles completed in one unit of time.
Inverse Sine
The inverse sine function (arcsine) is the inverse of the sine function. It is defined as the angle whose sine is a given value.
The formula for the inverse sine function is:
arcsin(x) = sin-1(x) = θ, where
1 ≤ x ≤ 1
Trigonometric Identities Involving Sine
Sine is involved in various trigonometric identities, including:
- Pythagorean Identity:sin 2(θ) + cos 2(θ) = 1
- Double-Angle Identity:sin(2θ) = 2sin(θ)cos(θ)
- Half-Angle Identity:sin(θ/2) = ±√((1 – cos(θ)) / 2)
Ending Remarks: Sine Definition
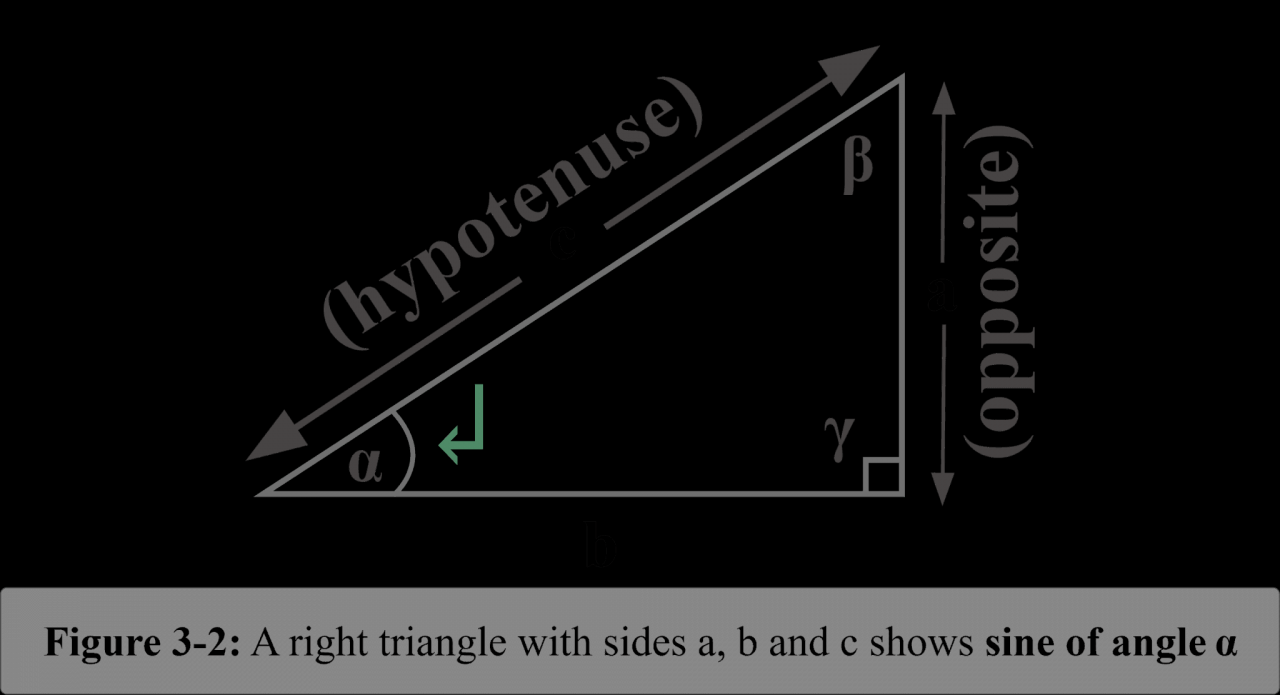
In conclusion, the sine function stands as a cornerstone of trigonometry, with its versatility extending across diverse disciplines. Its ability to model periodic phenomena and solve complex equations makes it an indispensable tool for scientists, engineers, and musicians alike. As we bid farewell to this exploration, may the knowledge gained serve as a beacon guiding your future endeavors in the realm of mathematics.
Quick FAQs
What is the formula for sine?
sin(θ) = opposite/hypotenuse
What is the range of the sine function?
[-1, 1]
What is the period of the sine function?
2π